比赛真的变简单了好多呢。

Backpack

题面

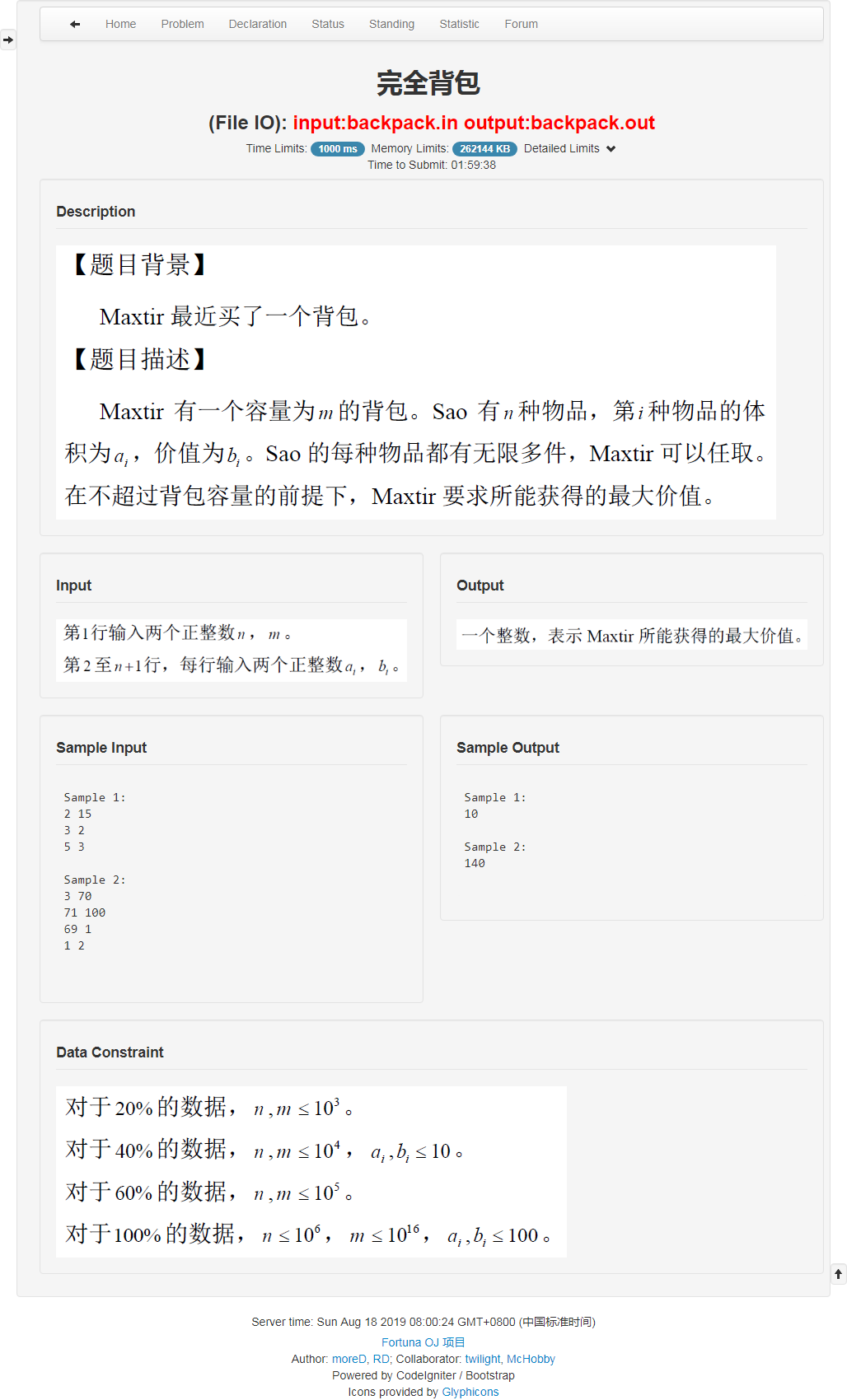
考场

首先想了一个贪心。（部分背包类似，把所有物品按照一个性价比排序。）

然后黑了自己。

然后开始 $dp$ ，发现是一个 $O(nm).$ ：

​ $\Large dp_j=\max\{dp_{j-w_i}+v_i\}.$

搞完后面的之后回头来看，发现 $a,b$ 的范围只有 $[1,100]$，那可以考虑做一个桶，把 $a$ 一样的物品只存它们的 $\max v.$

Slope

题面

考场

首先读了下题，题意是找出斜率最接近 $\large\frac{P}{Q}$ 过两点直线的斜率·。

那么直接看一下一条直线的斜率和 $\large \frac{P}{Q}$ 的差是什么：

​ $\Large \Delta=|\frac{P}{Q}-\frac{y_1-y_2}{x_1-x_2}|=|\frac{P(x_1-x_2)-Q(y_1-y_2)}{Q(x_1-x_2)}|=\frac 1 Q|\frac{(Px_1-Qy_1)-(Px_2-Qy_2)}{x_1-x_2}|.$

Vote

题面

考场

一开始觉得应该是越靠近旁边的越容易被选上，但是写了一个小程序一看不太对。发现已选一定人之后怎么求出他们中的贡献是一定要求的所以开始推这个式子。

首先考虑 $f_i$ 表示前 $i$ 个是选上的，那么向下一个转移。然后可以插一对进去，可以两个赞成，两个反对或者一个赞成一个反对。一个赞成一个反对可以直接转移，但是另外两种情况就不行了，然后我开始走弯路，走了很远很远。。（$f_{i,~j}$ 表示前 $i$ 个 $j$ 被选了没有之类的。。）

Count

题面

考场

主攻它！

首先因为它要求所有数不是 $m$ 的倍数，所以首先考虑容斥一下把 $m$ 扣掉。

大概的式子是这样的：

​ $\Large C_{n - 1}^{m - 1}-\sum\limits_{k=1}^{\frac {n}{m}}C_{n-km-1}^{m-1}-\sum\limits_{k=2}^{\frac {n}{m}}C_{n-km-1}^{m-2}-…$

Maze

题面

考场

第一眼看到了那个 $n$ 好像特别小，就想着能不能用 $n\times n$ 的正方形来分成很多很多块，然后一起做，至于询问的话想了一下线段树来维护边上的点到另一边点的最短距离（每个节点上开二维数组存），然后写广搜初始化和旁边的情况。至于线段树上的合并可以枚举一下中间从哪里走然后更新整个的答案。

因为好像走了就用不了 $jzoj$ 了所以不放比赛地址了。。

Math

题面

考场

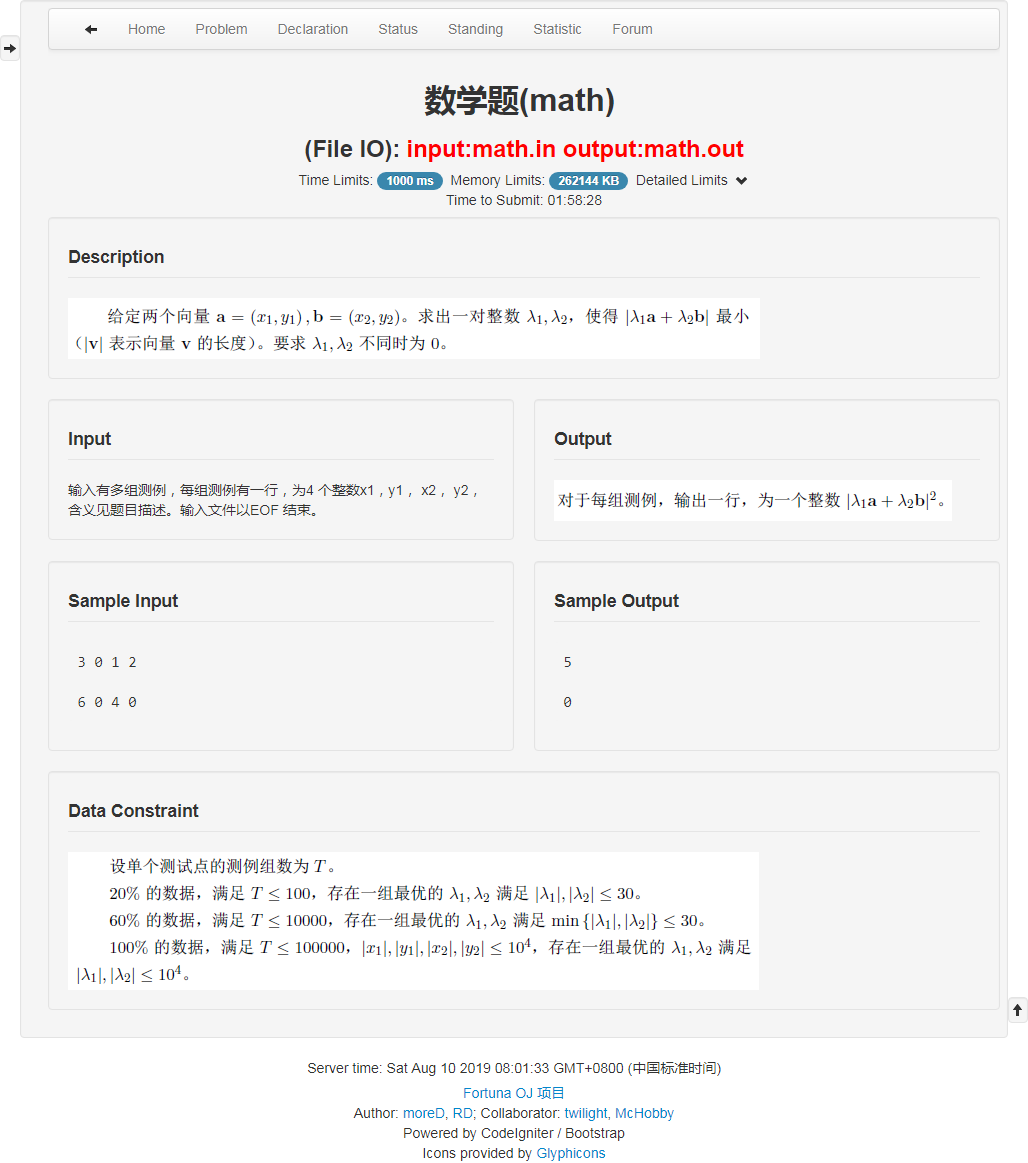
考场上主要玩这题了。能 $A$ 了就值了。。

首先朴素的把答案的式子展开：$\vec a=(x_1, y_1), ~\vec b = (x_2, y_2).$

​ $\large\begin{equation} \begin{aligned}Ans &=|\lambda_1\vec a+\lambda_2\vec b|^2\\&=(\lambda_1x_1+\lambda_2x_2)^2+(\lambda_1y_1+\lambda_2y_2)^2\ &=\lambda_1^2x_1^2+2\lambda_1\lambda_2x_1x_2+\lambda_2^2x_2^2+\lambda_1^2y_1^2+2\lambda_1\lambda_2y_1y_2+\lambda_2^2y_2^2 \ &=\lambda_1^2(x_1^2+y_1^2)+2\lambda_1\lambda_2(x_1x_2+y_1y_2)+\lambda_2^2(x_2^2+y_2^2)\end{aligned}\end{equation}$

比赛地址：http://jzoj.net/senior/#contest/home/2835

Cell

题面

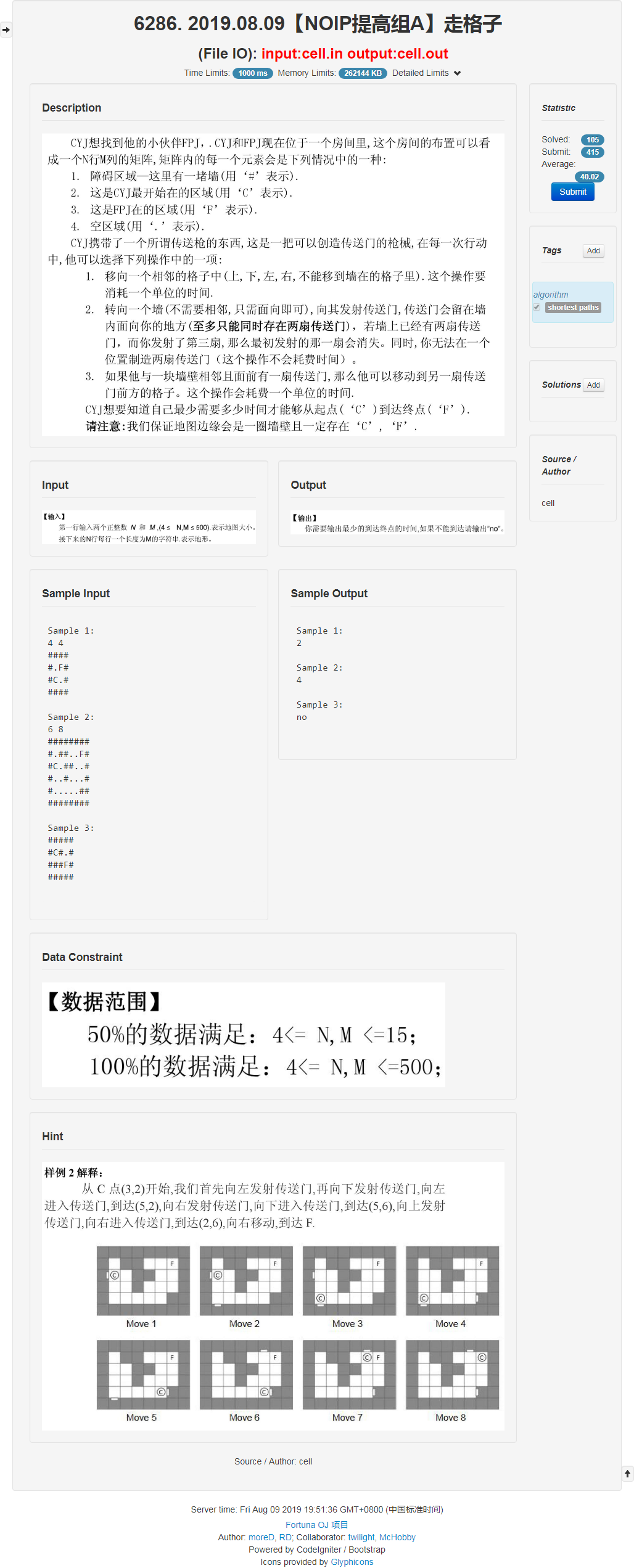
###　考场

比较简单的题吧，首先它给出了一种叫传送门的东西要走迷宫，就先看看传送门用来做什么。

它可以被开在墙上，然后在墙边上传送过去。

那么就相当于两个点由一条更近的路连在一起了，那么就考虑最短路，看这个可能连成稠密图，所以跑 $dijkstra$ 。

比赛链接：http://jzoj.net/senior/#contest/home/2833

Seq

题面

考场

题目变简单了。这道题一个递推式很显然地看出可以做矩乘。那考虑怎么构造矩阵。

因为他都是前面式子相乘得到的下一项，而递推式里的常数 $b_i$ 又在指数上，可以想到两个等底数的式子相乘就等于他们的指数相加。那么只需要在指数上做矩乘维护一个递推后的指数和就好了。

比赛地址：http://jzoj.net/senior/#contest/home/2831

Game

题面

考场

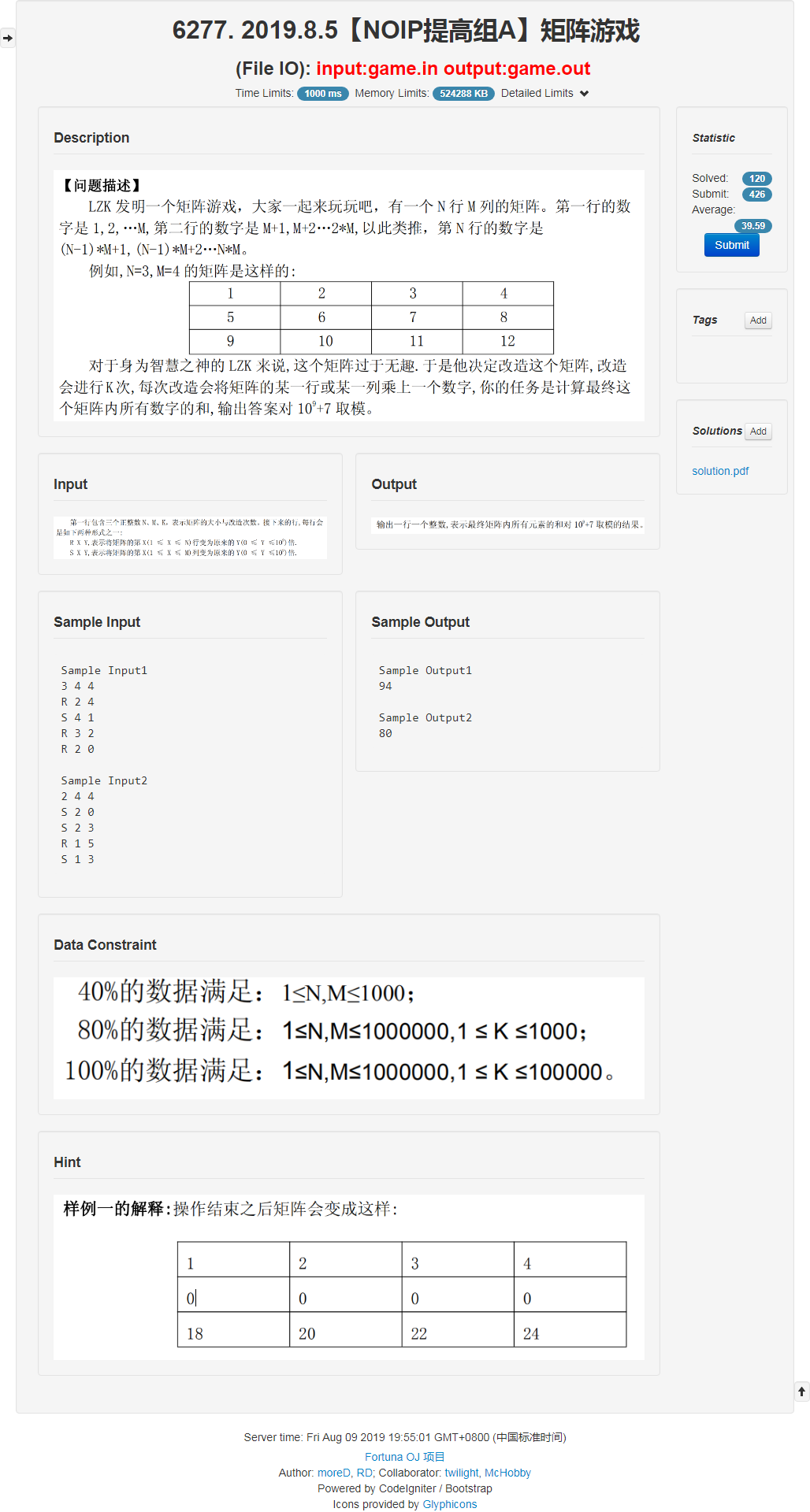
比较简单的数学题。//没想到第二道能 $A$ 的题就在今天。

首先发现 $n, m$ 都很大就肯定要行列分开的。因为你开一个数据结构空间也肯定爆了。

分开行列的时候观察每一个点上原始的数字是什么：

第 $i$ 行 $j$ 列是 $(i - 1)\times m+j$ 这个东西好像天然把行和列分开了。

比赛地址：http://jzoj.net/senior/#contest/home/2827

Forging

题面

考场

本来可以第一次考场上 $A$ 题，结果卡空间！我开了 $ll$ 就炸了！$int$ 就过了！而且他还卡常数。。（我 用 $cout$ 他最后一个点就 $T$ 了。）//终于可以考场正解一起写了。