比赛地址:http://jzoj.net/senior/#contest/home/2835
Cell
题面
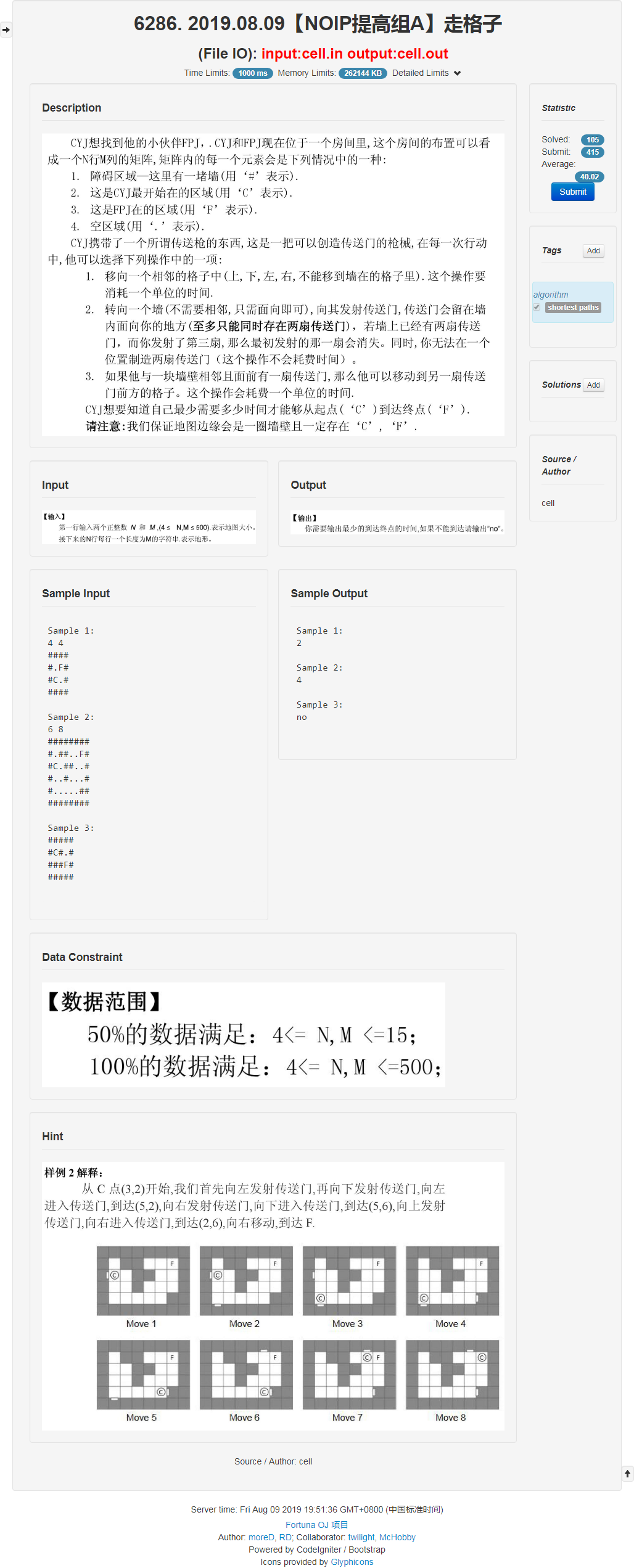
### 考场
比较简单的题吧,首先它给出了一种叫传送门的东西要走迷宫,就先看看传送门用来做什么。
它可以被开在墙上,然后在墙边上传送过去。
那么就相当于两个点由一条更近的路连在一起了,那么就考虑最短路,看这个可能连成稠密图,所以跑 $dijkstra$ 。
怎么建边呢?首先两个相邻的不是墙的点之间要连,长度为 $1$,另外在墙边上可以传到其他传送门去。所以墙边上就向每一个对着的墙前的空地连长度为 $1$ 的边。然后最短路。
出分: $0pt. RE$ ?????经过反复检查提交发现我在读图的时候用 $int$ 存了 $char.$ 但理论上没什么事啊。。$orz…$
改了之后还是没有 $A$ 为什么呢?
正解
仔细读题!发现第二项说明,就是建传送门的时候不需要和墙相邻!那么在四边没有墙的地方就也可以向某一边发传送门,然后走到另一个最近的墙,再在那座墙上开个传送门传到原来发了传送门的地方。也就是对于点 $(i, j)$ 向四个方向拓展到了墙是 $(x_k,y_k),k \in [0,3]$ 那么向每个点建长度为 $\min |x_k-i+y_k-j|+1$ 的边。(这里最近的点可能建了更远的边,但是没关系,因为我们可以直接用以前建好了的相邻空地的边走过去。)
$code: $ https://paste.ubuntu.com/p/hbSPW2jsFJ/
原题:jzoj5781
Tree
题面
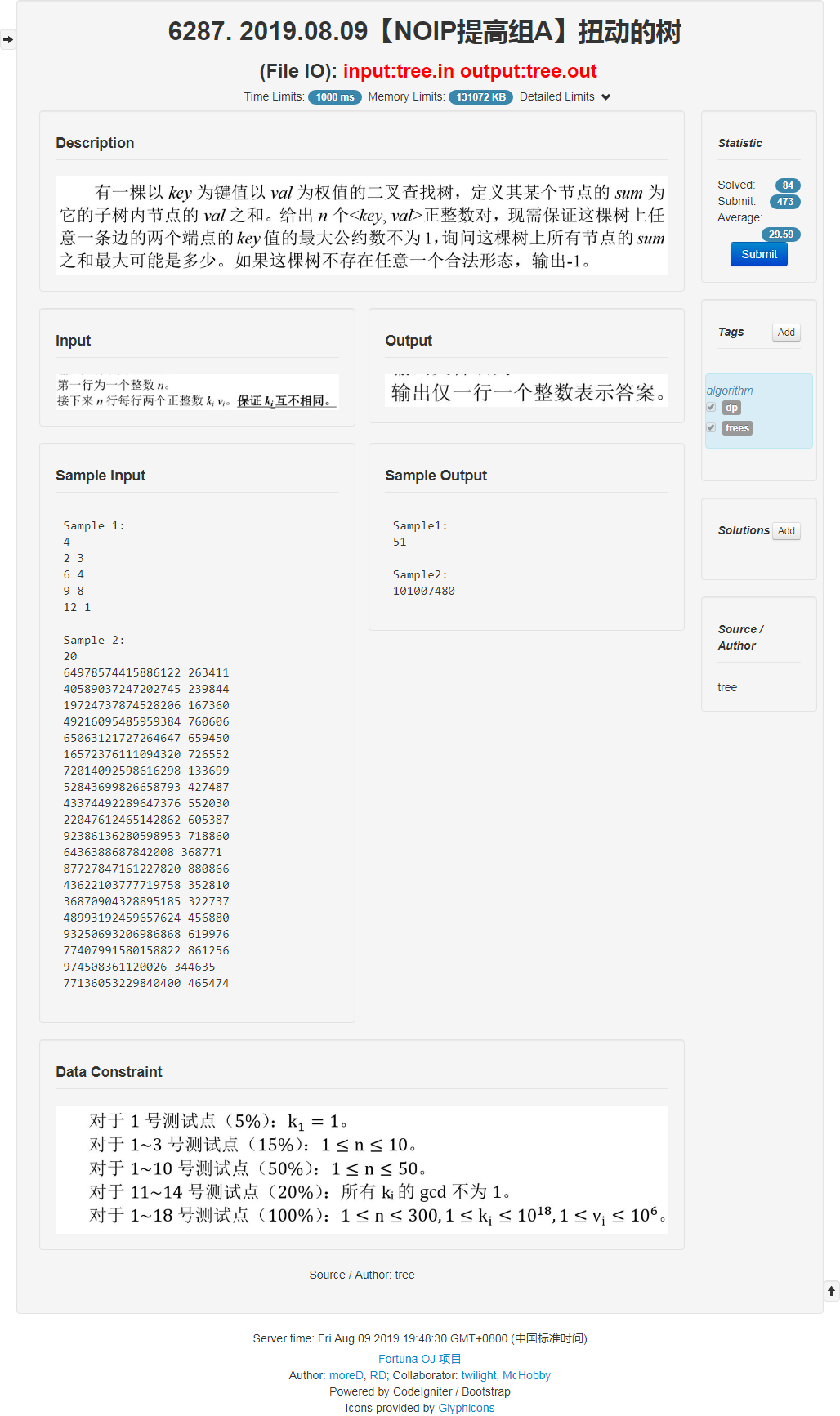
考场
这个,好复杂,没什么想法。。
考虑一下随机吧!既然是二叉搜索树,$n$ 也很小,那就考虑每次随即一个插入顺序,暴力插入更新答案?
可以的,第二个样例天差地别。。
不管了看 $T3$ 了。。
出分:$5pt..emm…$ 随机化一分没有。。//特判第一个点的 $5pt…$
正解
因为一个二叉搜索树的根可以相当于有序序列上的一个中间点,左边的区间就是左子树,右边的区间就是右子树。因为一个区间 $[l,~r]$ 只可能挂在 $l-1$ 的右边或者挂在 $r+1$ 的左边。所以我们记一下一个区间是挂在哪个爸爸上的。然后我们是知道整棵树的答案,所以可以类似区间 $dp$ 来做。
首先 $f_{l,r,0/1}$ 表示一段区间左端点($0$)或右端点($1$)是爸爸,自己就是 $[l+1,r]$ 或者 $[l,r - 1].$ 那么考虑一个普通的区间 $dp$ 是怎么转移的。 首先枚举左端点和右端点,那么我们考虑怎么转移,这里因为是可以把自己的爸爸挂在它爸爸的左边或者右边,再考虑向 $f_{l-1,r,0}$ 和 $f_{l,r-1,1}$ 转移,就有方程: $\Large f_{l-1,r,0}=\max f_{l,k,1}+f_{k,r,0}+\sum_{i=l}^{r}K_i,\quad \gcd(K_{l-1},K_k)>1\\\Large f_{l,r +1,0}=\max f_{l,k,1}+f_{k,r,0}+\sum_{i=l}^{r}K_i,\quad \gcd(K_{r+1},K_k)>1$
后面的区间和考虑用前缀和预处理即可。并且如果每一次求 $\gcd$ 也会 $T$ 掉,所以两两间的 $\gcd$ 也要预处理。$k$ 跟另外答案是 $\max f_{1,i,1}+f_{i,n,0}.$
$code: $ https://paste.ubuntu.com/p/f2wk9GBwJX/
Rotate
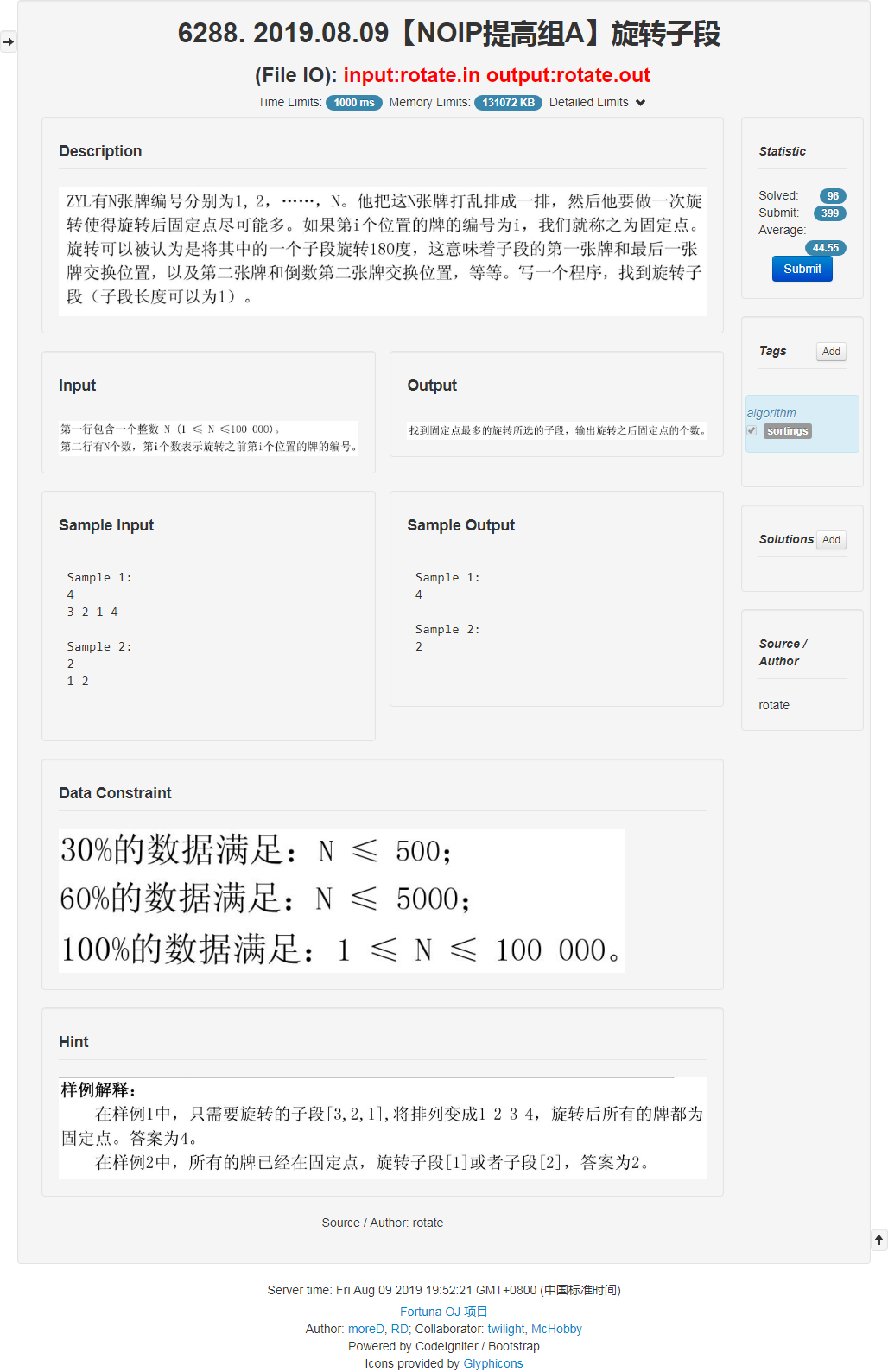
考场
题意很简单,先考虑第一个 $30pt.$: $O(n^3)$ 暴力:暴力选区间,暴力反转,暴力找对数。
然后看第二个数据点是个 $O(n^2)$ 的做法,那考虑优化上面那个暴力:不需要暴力找了,可以固定一个中间点,然后一对一对向外面扩展,没扩展一层更新答案。这就有 $60pt.$ 了。(卡到了 $65pt..$)
最后要交题的时候准备推一下一个点到自己的对应位置的式子,发现对于每个点有:
对于点 $i$ 要去的点是 $a_i$ ,如果关于 $k_i$ 对称过去,那么有 $i+a_i=2k_i.$
然后发现左边的每个点是固定的,所以对应 $k_i$ 也是固定的,那么考虑一下反转区间,发现反转区间的左右端点肯定是有一个固定点的,因为没有的话就没必要扩展开,不扩展是不劣的。(可能把固定点翻没了。)那就可以考虑每一个点的这个 $k_i$ ,更新答案,所以我们需要维护的是反转区间里面 $k_j=k_i$ 的点的个数,反转区间外的前后缀和解决。这个可以用根号算法解决,比如分块?莫队?
分块写的快些所以当时写的分块,但是没调出来。就算调出来了也要爆空间。。
交的平方暴力。
出分:$65pt.$
正解
莫队($O(n\sqrt n)$)
上面讲的够清楚了,接下来就是把那些反转区间的询问用莫队搞一搞了。应该就是模板了,只需要询问区间内某个数的出现次数即可。//注意维护的是 $v_i$ 也就是 $a_i+i~!!!$
$code:$ https://paste.ubuntu.com/p/nB6h7KSrbx/
优化上面的平方暴力?($O(n\log n)$,$\log$ 数据结构(其实可以排序降一点)。)
首先上面分块的时候说过一个反转序列的左右端点一定在反转之后是一个不动点,然后就可以记一下一个点的不动点在哪里,挂在那个中间点后面,然后在枚举中间点的时候就可以左右跳只跳到不动点的位置更新答案,这里因为要顺着跳,所以可以用一个大根堆记左端点(或小根堆记右端点),然后一个个跳着更新答案就可以了。因为只有 $n$ 个点,所以只会跳 $n$ 次,加上堆的复杂度就是 $O(n\log n).$
其实复杂度瓶颈在让每个点后面的数有序,其实用一个线性排序算法就可以总体线性了。(基数排序。?)