比赛地址:http://jzoj.net/senior/#contest/home/2831
Game
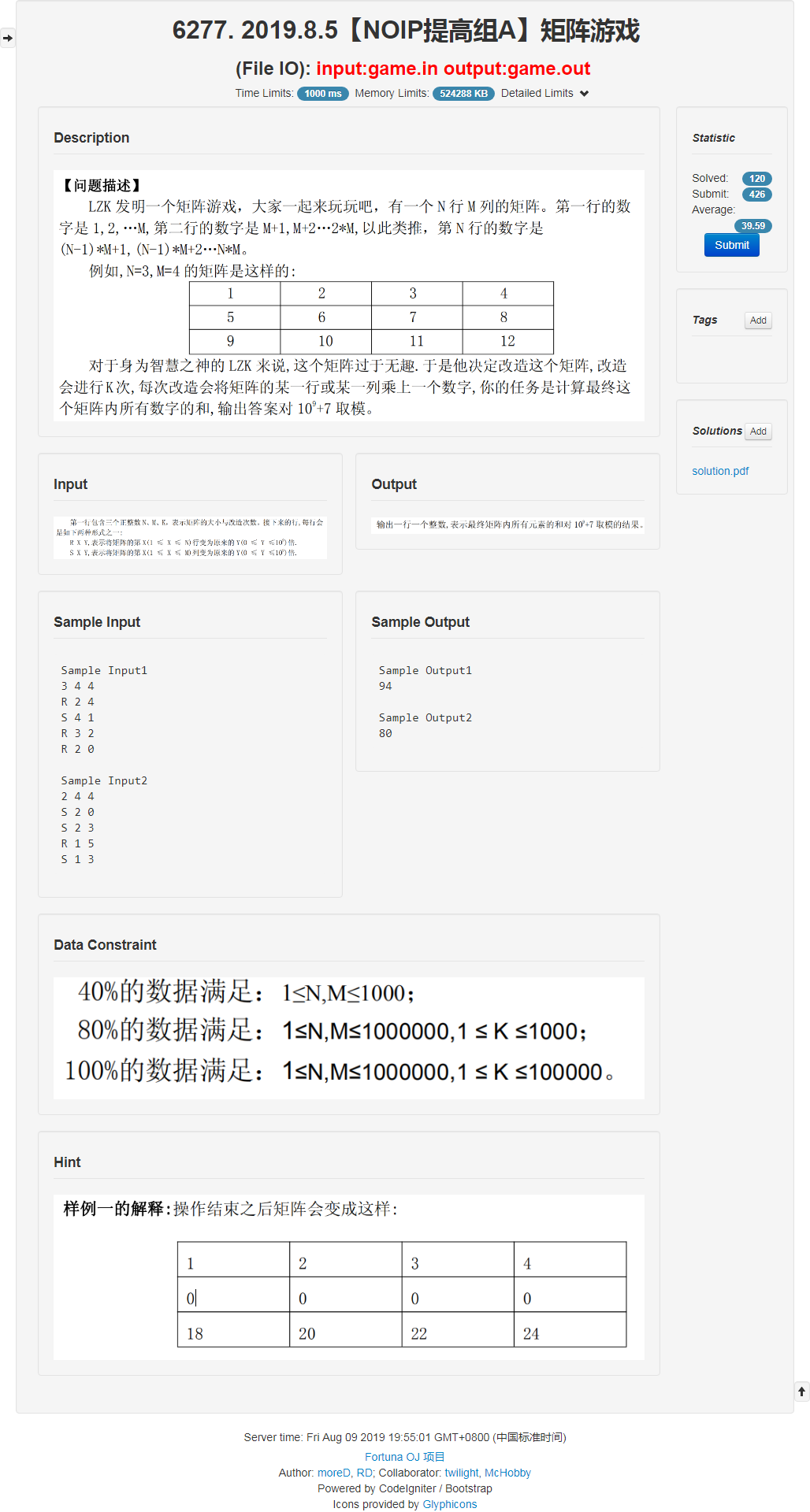
题面
考场
比较简单的数学题。//没想到第二道能 $A$ 的题就在今天。
首先发现 $n, m$ 都很大就肯定要行列分开的。因为你开一个数据结构空间也肯定爆了。
分开行列的时候观察每一个点上原始的数字是什么:
第 $i$ 行 $j$ 列是 $(i - 1)\times m+j$ 这个东西好像天然把行和列分开了。
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
那么我们试着把一张表拆成两张表, 其中一张表是加号前的那项, 另一张是加号后的。(这样做的另一个动机是每一列可以看做是 $m$ 的一个剩余系了。)
表 $1$ :
| 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 |
表 $2$ :
| 0 | 0 | 0 | 0 |
| 4 | 4 | 4 | 4 |
| 8 | 8 | 8 | 8 |
其实这样对应相加也能得到原始表格。那么根据乘法分配律, 所有操作可以分别对两个表进行之后求和相加即可得到原表格的答案。
然后发现表 $1$ 里面的每一列是相同的, 表 $2$ 中的数是相同的。所以表 $1$ 中只需要将列的修改做成一个倍数和, 从行的方向扫一遍, 并将它和行的修改以及这一列的数字一起乘起来就是结果了。表 $2$ 中同理。
这样的复杂度就只有 $O(n+m)$ 了, 然后 $n,m$ 同级所以就是线性的了。
出分:$40pt.$ 我求倍数和的时候没取模爆炸了!!!!
加了就 $A$ 了。
$code:$ https://paste.ubuntu.com/p/CpJXw6vXhR/
Jump
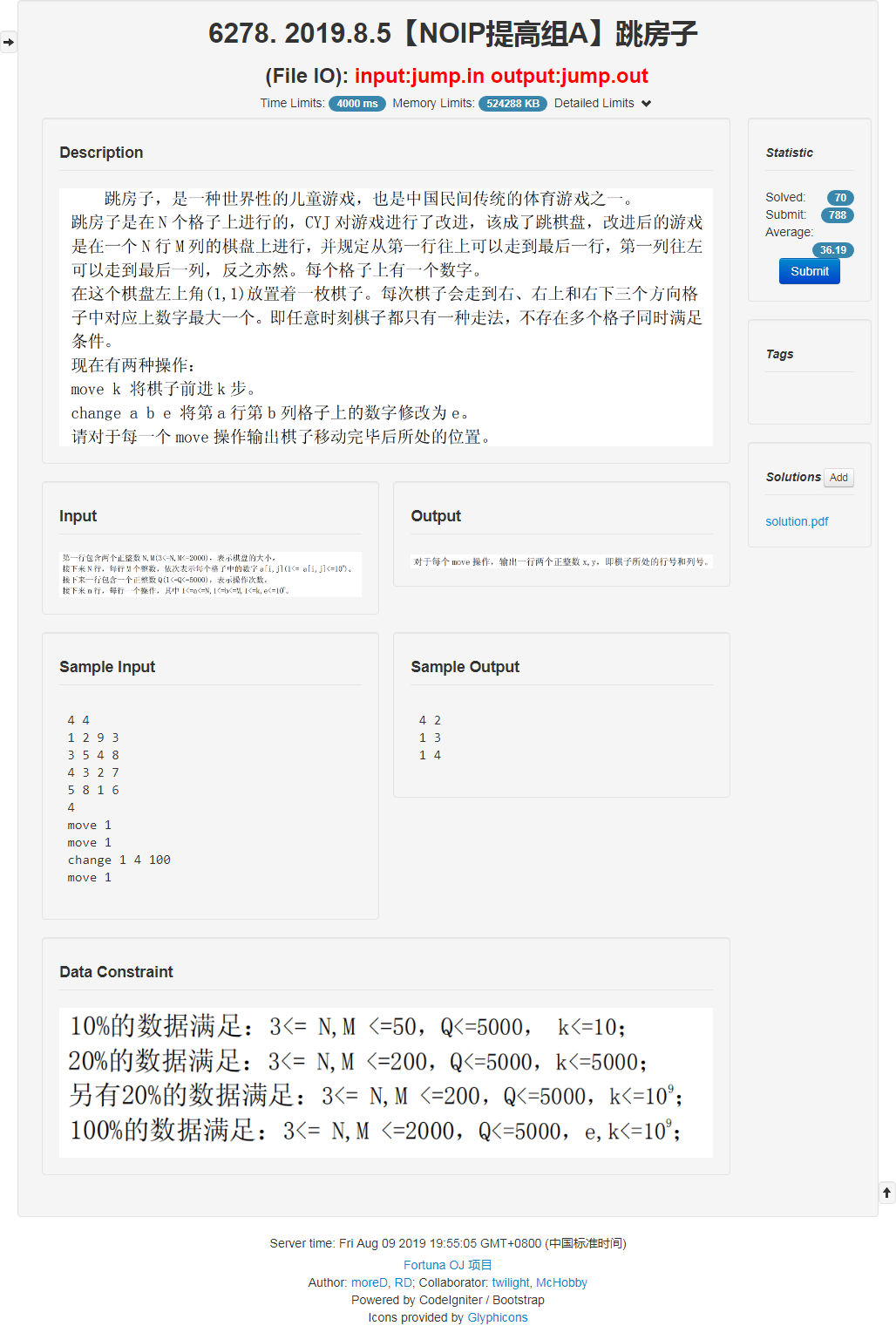
题面
考场
这个。一个数好像只能向一个地方走, 那就是 $n$ 个点, $n$ 条边, 就是一颗基环外向树啊?
那么一定有循环了。但是找循环应该是 $O(nm)$ 级别的, 待修改的话就起飞了。
那考虑修改怎么改。因为是一颗基环外向树, 那么边只可能是树边和环边了, 那分类讨论一下:
1. 树边重新接在树上:对环(循环)没有影响直接连.
2. 树边重新接在环上:还是没有影响.
3. 环边重新接在树上:环变大了.搜一下变大的部分.
4. 环边重新接在环上:环变小了.搜一下变成树的部分.然后开始写。然后就没时间了。然后发现这样写每一次修改都要带着 $O(nm)$ 这个肯定就会爆炸了。
然后跟暴力拍 $1$ 个点就 $WA$ 了。细节写挂了吧。。
出分:$20pt.$ (交的暴力。)
正解
就是高效地找循环搞循环。
因为循环是 $O(nm)$ 的而且每跳过 $n$ 步所在的一列是重复的。所以我们分块一下, 每一块的长度是 $L =\min (n, m)$ , (这个东西如果 $m$ 比 $n$ 大手动交换它们。)每一次一大块一大块地跳来找循环节, 不在大块顶点就暴力跳。这样找循环的复杂度就是 $O(L).$ 然后一个小优化就是只需要在修改后的第一次查询处找一次循环节。
那修改操作呢。修改操作应该是会去有可能改到前三个点的范围内的答案的, 然后我们分别看每一个点, 首先看它改到了哪一个点, 先从那个点往后跳跳到块地端点上, 然后向前跳, 向前跳发现可能前面的几个数都跳到这里了, 那么发现我们可以从中间向外扩展, 每次只考虑上下界的转移, 因为中间的只能看到后面三个包含在我们考虑区间内的, 一定能走到后面的点上的。(如果连第一行都走不到就不用更新了。)
但是他有一个 $3$ 的常数?//其实我怎么看这个都会 $T…$
$code: $
原题。?
$luogu$ 原题链接:[https://www.luogu.org/problem/P4739](它开 $8s$ 比赛开 $4s$ ?)
[https://www.luogu.org/problem/P4739] :https://www.luogu.org/problem/P4739
Sequence
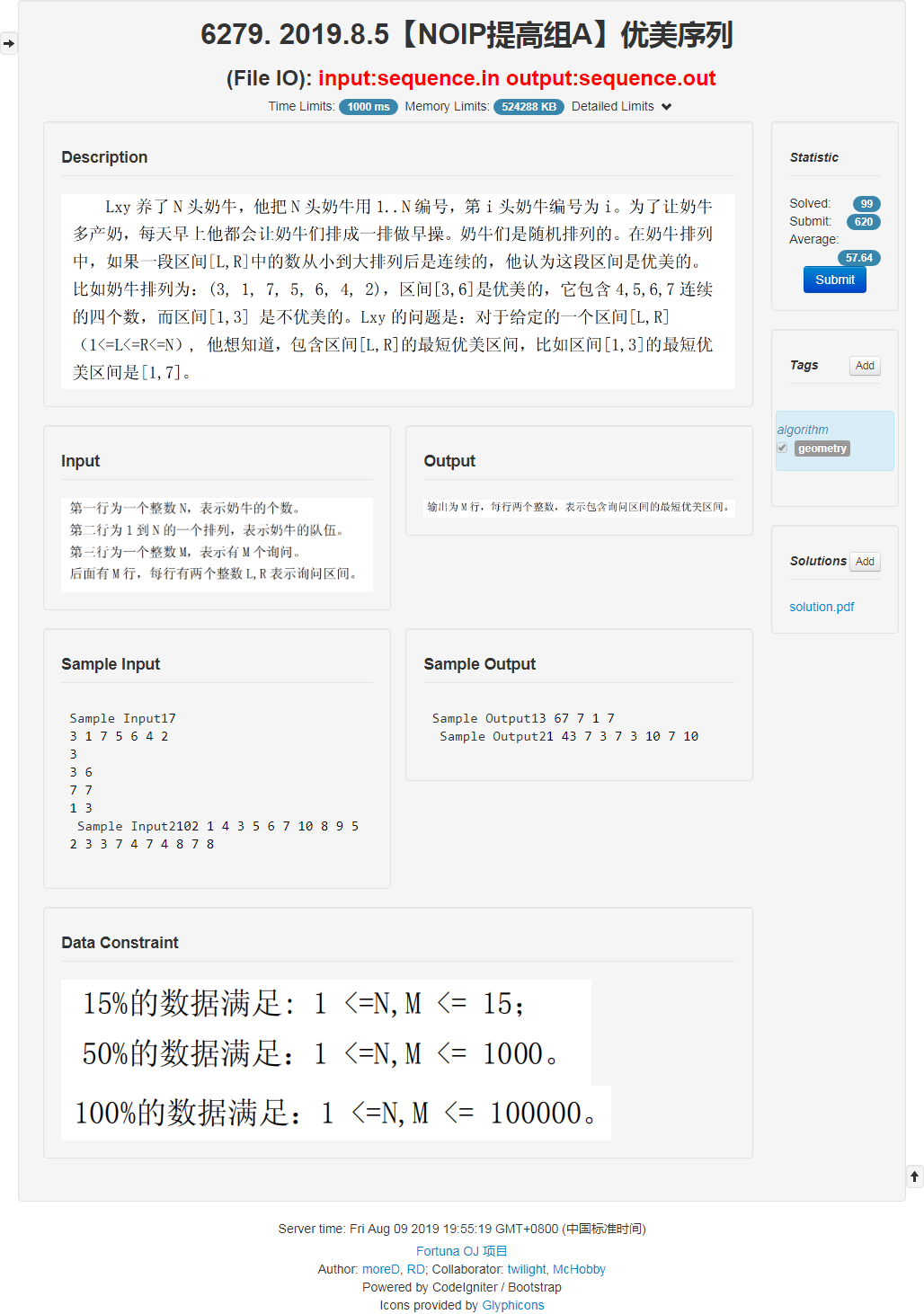
题面
考场
想着用线段树 $Hash$ , (我傻啊又没有重复。。)写了 $WA$ 掉了的暴力。//没时间了。。
出分:$0pt…$
正解
$80pt.$$100pt.$ 的卡常线段树 $/ ST$表
因为要是一段优美的序列 $a_{i…j}$, 里面的就需要是 $[\min_{i…j},\max_{i…j}~]$ 中的所有数都要包含在内的, 就是说
$[\min_{i…j},\max_{i…j}~]$ 中即使是最左边和最右边的数都要在这个范围内, 因为他已经天然离散化了, 所以可以根据一个数字出现的位置得到一个新序列, 而优美的序列就是说两个序列的长度是一样的。这样通过反复地来回映射就可以找到一个最短的包含自己的序列了。(因为每一次映射都是一个必须满足的条件得到的一个新区间, 而区间长度递增, 所以第一次的就是最短的。)
$eg.$
$\quad A~=\{ 3,1,7,5,6,4,2\}\\
\quad A’=\{ 2,7, 1,6,4,5,3\}$
那么例如 $[3, 6]$ 就是一段优美的序列, 因为 $A$ 序列中的最大最小值对应区间 $[4,7]$ 长度和原序列中的 $[3,6]$ 长度都是 $4.$
那么我们就是需要查询两个序列的区间最值, 线段树 $/~ST$ 表, 因为线段树查询带 $log$ 而且常数大, $ST$ 表肯定就是更好的选择。
分治
没人会。。题解讲的好像很随意。网上说得好像用线段树扫描线?
严格 $log$ 的线段树
考虑一个优美序列满足什么样的性质。首先它肯定是由连续数字组成的。(废话那是定义。)
称每两个连续数字是一个连续数对的话,那么对于一个优美序列而言就有:
$l+num=r ~IFF ~a_{l,…,r}是一个优美序列$.(其中 $num$ 是连续数对个数)
证明的话这个东西显然的:排好序之后是从 $Min$ 到 $Max$ 的一个连续序列, 中间自然就有 $r-l$ 个连续数对了, 逆命题同理。
然后我们考虑怎么维护这个信息。可以首先考虑把询问离线下来并从左往右考虑右端点 $i$ 框定包含询问的右端点的优美序列。 这样首先可以保证右边的 $r$ 是一个有序的。
然后考虑每一次来到一个右端点 $r$ 的时候考虑用它所组成的连续数对更新能够成立的等式左边就可以了。这样的话首先考虑每个点初始就会有一个自己位置的值 $pos.$ 然后通过后面和它后面的数(包括它)构成的连续点对更新自己的值以得到答案。那么每次的右端点更新左边的值就是更新一个前缀和,那么区间加。
再考虑怎么得到答案。每次需要的是最右边的一个在询问的左端点左边的点,那么怎么保证呢?观察式子的左边,发现这个东西每一次可能受到 $+0,+1,+2$ 三种影响,这个不太好处理,而考虑到每一次右边是肯定会 $+1$ 的,所以我们考虑改变的差值。差值就只可能 $-1,+0,+1$ 因为 $num$ 初始为 $0$ 时左边是小于右边的,而每次 $+1$ 就又可以保证这个差值是一个一个缩小的,所以如果出现了答案,这个值一定是整个前缀中最大的之一。那么区间最大值。
区间加 $+$ 区间最大值:线段树。 $\rightarrow$ 严格 $O(n\log n)$ 算法。
$code: $ https://paste.ubuntu.com/p/WgP6sm3MQH/
原题。??
$luogu$ 原题链接:https://www.luogu.org/problem/P4747(它开 $3s$ 比赛开 $1s$ ???)