因为好像走了就用不了 $jzoj$ 了所以不放比赛地址了。。
Math
题面
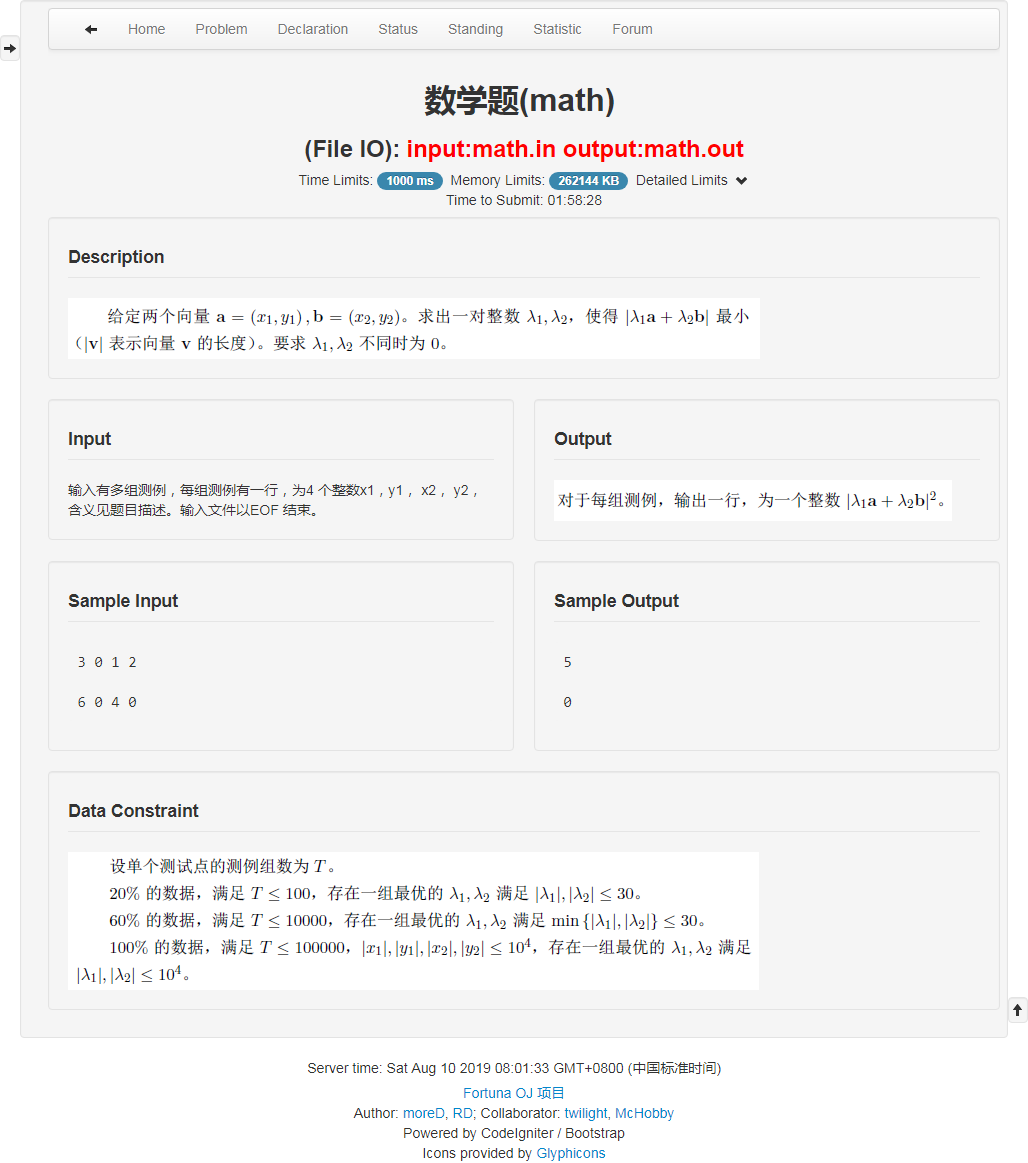
考场
考场上主要玩这题了。能 $A$ 了就值了。。
首先朴素的把答案的式子展开:$\vec a=(x_1, y_1), ~\vec b = (x_2, y_2).$
$\large\begin{equation} \begin{aligned}Ans &=|\lambda_1\vec a+\lambda_2\vec b|^2\\&=(\lambda_1x_1+\lambda_2x_2)^2+(\lambda_1y_1+\lambda_2y_2)^2\ &=\lambda_1^2x_1^2+2\lambda_1\lambda_2x_1x_2+\lambda_2^2x_2^2+\lambda_1^2y_1^2+2\lambda_1\lambda_2y_1y_2+\lambda_2^2y_2^2 \ &=\lambda_1^2(x_1^2+y_1^2)+2\lambda_1\lambda_2(x_1x_2+y_1y_2)+\lambda_2^2(x_2^2+y_2^2)\end{aligned}\end{equation}$
然后因为 $\vec a, \vec b$ 是给定的,所以可以记 $\large a=x_1^2+y_1^2,b=x_1x_2+y_1y_2,~c=x_2^2+y_2^2.$
那么式子就变成了:$\large Ans =a\lambda_1^2+2b\lambda_1\lambda_2+c\lambda_2^2$,然后我们研究右边。
首先有 $a\geq 0$ 所以把右边配成定点式有:$\large a(\lambda_1+\frac b a \lambda_2)^2+\frac{ac-b^2}a \lambda_2^2 \geq \frac{ac-b^2}a \lambda_2^2$
它有什么用呢?
首先,如果我们枚举一个 $\lambda_2$ 的话,我们就可以通过取 $\lambda_1$ 顶点 $\frac a b\lambda_2$ 附近的两个值就是最小值了。进一步可以发现,因为包含 $\lambda_2$ 的项有平方,而 $\lambda_1$ 又可以根据它来取,所以可以令 $\lambda_2\geq 0$ ,这样它小于零的情况可以通过把 $\lambda_1$ 取反等效成大于零。
其次,我们继续观察它的顶点纵坐标 $\frac{ac-b^2}a \lambda_2^2$ 。因为我们取的 $\lambda_2$ 是递增的自然数,所以它的平方递增的速度就非常快了,那么我们看看它的系数是不是也是非负的,这样就可以提很多速了。首先下面是非负的,也就是正的了,那么上面可以:
$\large\begin{equation} \begin{aligned}ac-b^2&=(x_1^2+y_1^2)(x_2^2+y_2^2)-(x_1x_2+y_1y_2)^2\\&=x_1^2x_2^2+x_1^2y_2^2+y_1^2x_2^2+y_1^2y_2^2-x_1^2x_2^2-2x_1x_2y_1y_2-y_1^2y_2^2\\&=x_1^2y_2^2+y_1^2x_2^2-2x_1x_2y_1y_2\ &=(x_1y_2+x_2y_1)^2\geq0.\end{aligned}\end{equation}$
好的!它是非负的。所以就可以这样做啦!
然后开始和纯暴力拍,拍了一会改了些错发现没什么问题。
然后随机了几组数据发现跑的飞快。($300ms\sim500ms $ 加个 $O(2)$ 估计会很快)
出分:$100pt.$ //数据有点水,我这个算法应该能被卡的。
$code: $ https://paste.ubuntu.com/p/x3m5FqDWCw/
正解
那个算法很奇妙,所以还是好好写一下。
首先它是从欧几里得算法过来的。(靠虑共线的时候就是 $\gcd$ 最小。($ax+by=1.$))
我们考虑两条向量的夹角到一定程度之后是什么样的。还是从答案出发,这次用点乘:
$\large\begin{equation}\begin{aligned}Ans&=|\lambda_1\vec a+\lambda_2\vec b|^2\ &=\lambda_1^2|\vec a|^2+\lambda_2^2|\vec b|^2+2\lambda_1\lambda_2|\vec a·\vec b|\ &=\lambda_1^2|\vec a|^2+\lambda_2^2|\vec b|^2+2\lambda_1\lambda_2|\vec a||\vec b|\cos\ang\theta.\end{aligned}\end{equation}$
其中 $\theta$ 就是夹角了,我们想把前面的 $2$ 消掉?那 $\theta$ 取 $60^\circ$?
$\large\begin{equation}\begin{aligned}Ans&= \lambda_1^2|\vec a|^2+\lambda_2^2|\vec b|^2+2\lambda_1\lambda_2|\vec a||\vec b|(-\frac1 2)\\&=\lambda_1^2|\vec a|^2+\lambda_2^2|\vec b|^2-\lambda_1\lambda_2|\vec a||\vec b|.\end{aligned}\end{equation}$
两个 $\lambda$ 分别取 $0$ 的时候坑定是另一项取 $1$ 最优,那不就是等于 $\vec a^2$ 或 $\vec b^2$?
那么不取零的时候呢?考虑配方:
$\large\begin{equation}\begin{aligned}Ans&\geq|\lambda_1^2\vec a|^2+|\lambda_2^2\vec b|^2-|\lambda_1\vec a||\lambda_2\vec b|\\&=(|\lambda_1\vec a|-|\lambda_2\vec b|)^2+|\lambda_1\vec a||\lambda_2\vec b|\\&\geq|\lambda_1\vec a||\lambda_2\vec b|\geq|\vec a||\vec b|.\end{aligned}\end{equation}$
那我们不妨设 $|\vec a|\geq|\vec b|$ 就有:
$\large Ans \geq \vec a^2.$
$OK$ 了!
而当夹角更大的时候 $\cos \theta$ 是减小的所以那个东西是大于等于这个六十度的时候,所以同理了。
也就是说把角度搞到 $60^\circ$ 以上就好了?那我们怎么改角度呢?因为我们的 $\lambda$ 是任取的,所以两个向量分别加上一定倍数的对方是没有影响的。(可以通过减对方减回来。)
即 $Ans\{\vec a,\vec b\}=Ans\{\vec a,\vec b+k\vec a\}.$
好的那么我们构造一下。
这里记 $\vec a=\vec{OA},~\vec b = \vec{OB}$,其中 $|\vec a| \leq |\vec b|$考虑两个向量的差 $\vec c=k\vec a-\vec b$ ,那么我们可以直接求 $Ans\{\vec a , ~\vec c\}$ 即可,那么怎么取 $k$ 可以让夹角尽量大呢?
考虑向量 $\vec b$ 在 $\vec a$ 所在直线上的投影点 $K$ ,然后考虑 $k\vec a$ 在 $K$ 附近,这里假设 $k\vec a=\vec{OA’},~(k+1)\vec a=\vec{OA’’}$ ,而 $K$ 在 $A’A’’$ 上。则:
如果 $|k|=1$ ,那么直接取它就好。
不然的话考虑哪一个更优,就比较 $BA’$ 和 $BA’’$ 的大小就好。
但其实实现上来说直接取 $k\vec a$ 就够了。
这样慢慢增大夹角直到大于 $60^\circ$ 的话,就相当于是欧几里得里面的不断取模,最后得到答案。
这个复杂度作者也不会证,但是几次就能得到答案的,因为每次增加的角不小。(作者猜测 $log$ 级)
这个复杂度就比上面的剪枝靠谱多了。
$code:$
Treasure
题面
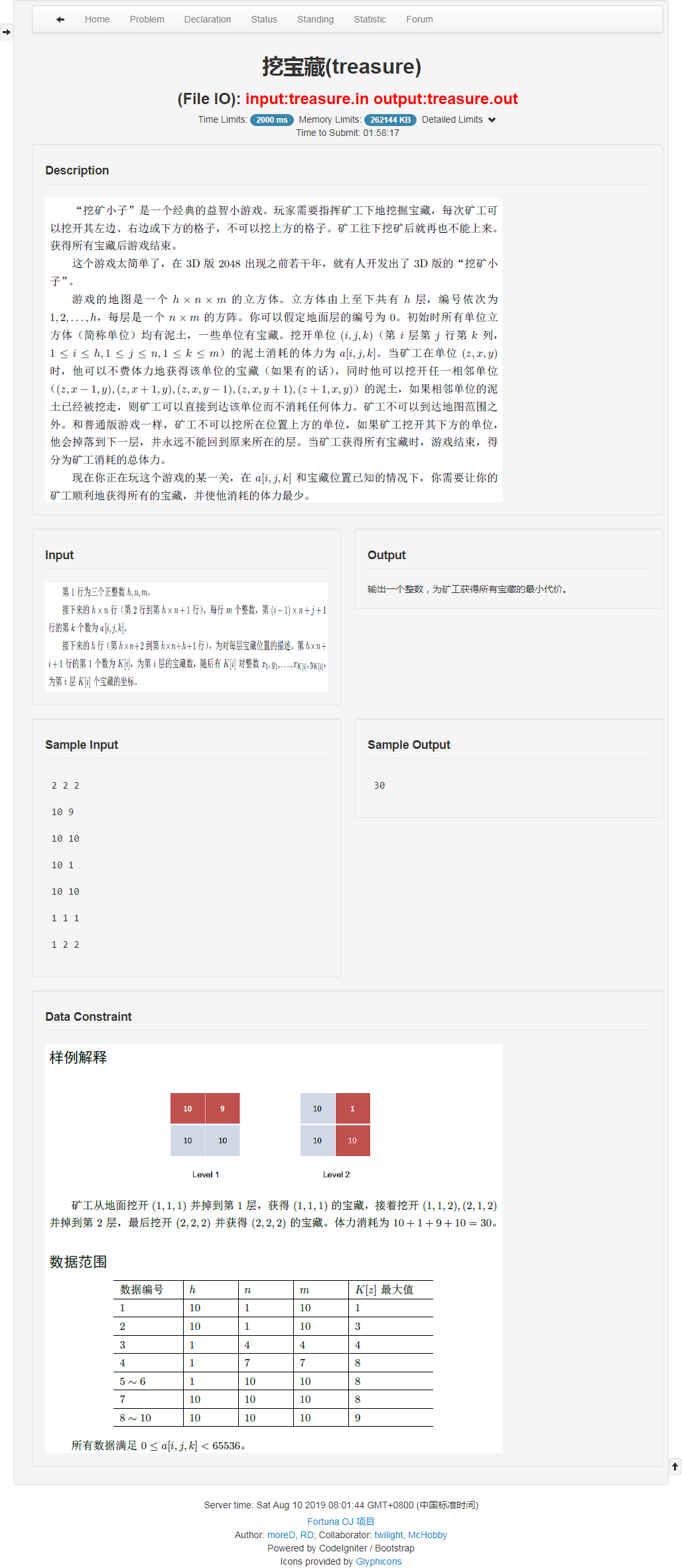
考场
一看就是爆搜?写了写前两个点,自己造的小数据过了,就没管了。
具体做法就是每一层记录最左最右的宝藏位置,那么他们之间的一定挖过了。然后暴力看走那个就好。
出分:$0pt.$
正解
好像是用斯坦纳树,看了博客不太会。咕。
City
题面
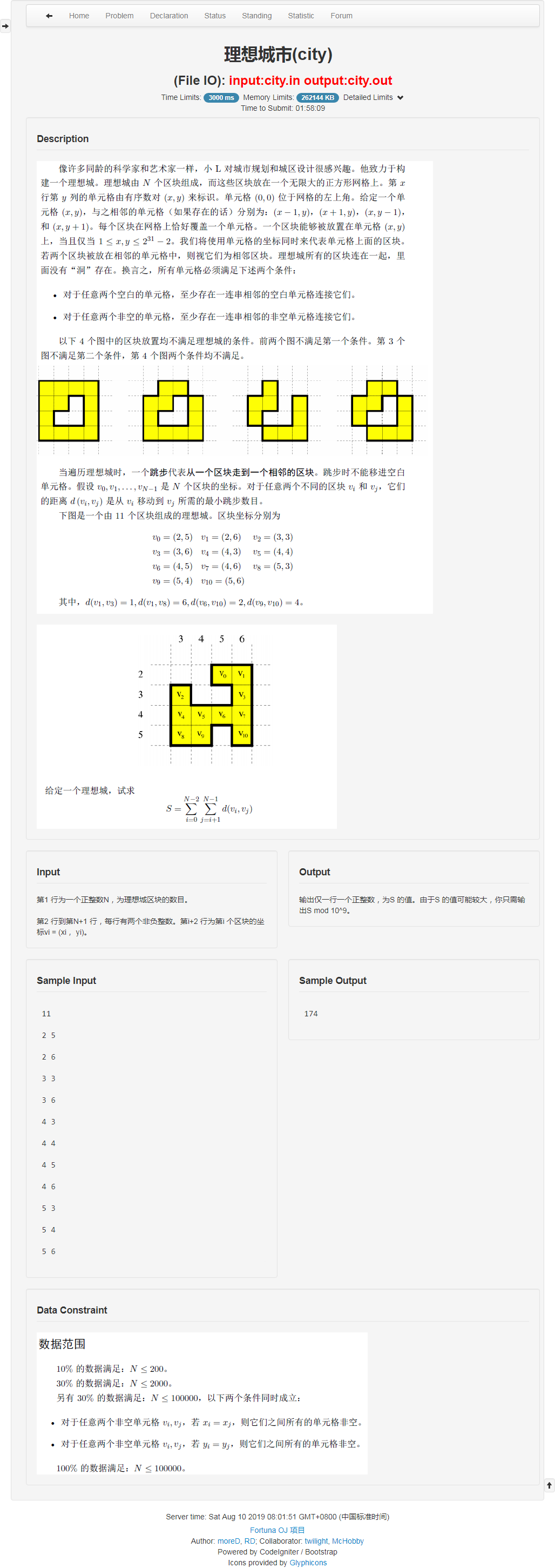
考场
建树$+DP$ ?
写了写一个倍增求路径和但是是错的。
出分:$0pt.$
正解
这是个 $IOI2012Day2T1$???
做法还是挺有意思的。
我们考虑如果是一棵树怎么办。就直接树形 $DP$ ,对于一个点 $now$ 记其子树大小 $siz$ ,我们考虑它和父亲连的边的贡献就是 $siz\times(n-siz).$
那么这道题呢?考虑把它变成树,而我们每一次只考虑横着的或者纵着的联通块。这样就能分别处理出竖向边和横向边分别的贡献,然后累加即可。
是的。就是如此简单,至于横纵交换交换一下横纵坐标即可。